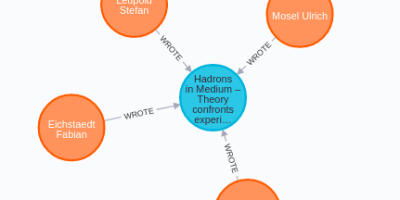
Centrality, Graph Algorithms, Graph data science, Neo4j, NLP

Centrality, Graph Algorithms, Graph data science, Neo4j, NLP
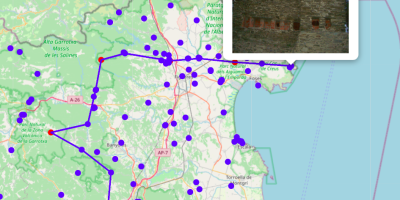
Graph Algorithms, Graph data science, mapbox, Neo4j, Spatial
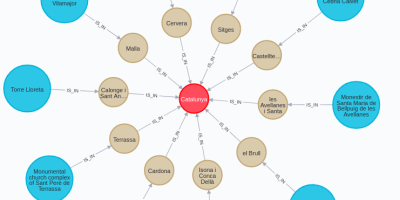
Graph Algorithms, Graph data science, Neo4j, Spatial
